Tutorial Pearsons Chi square Test for Independence. Ling 3. 00, Fall 2. What is the Chi square test for The Chi square test is intended to test how likely it is that an observed distribution is due to chance. This lesson describes when and how to conduct a chisquare test of homogeneity. Key points are illustrated by a sample problem with solution. Taskkill Windows 2000. Certificate Program in Biostatistics Epidemiology, Controlled Trials, Enviromental Statistics, aimed at those who need to understand the statistical methods. ChiSquareWordle.png' alt='C Program Chi Square Test' title='C Program Chi Square Test' />It is also called a goodness of fit statistic, because it measures how well the observed distribution of data fits with the distribution that is expected if the variables are independent. A Chi square test is designed to analyze categorical data. That means that the data has been counted and divided into categories. It will not work with parametric or continuous data such as height in inches. For example, if you want to test whether attending class influences how students perform on an exam, using test scores from 0 1. Chi square test. However, arranging students into the categories Pass and Fail would. Additionally, the data in a Chi square grid should not be in the form of percentages, or anything other than frequency count data. Thus, by dividing a class of 5. Pass. Fail. Attended. Skipped. 81. 5IMPORTANT Be very careful when constructing your categories A Chi square test can tell you information based on how you divide up the data. However, it cannot tell you whether the categories you constructed are meaningful. For example, if you are working with data on groups of people, you can divide them into age groups 1. Chi square test will treat the divisions between those categories exactly the same as the divisions between male and female, or alive and dead Its up to you to assess whether your categories make sense, and whether the difference for example between age 2. This does not mean that categories based on age are a bad idea, but only that you need to be aware of the control you have over organizing data of that sort. Another way to describe the Chi square test is that it tests. The test compares the observed data to a model that distributes the data according to the expectation that the variables are independent. Wherever the observed data doesnt fit the model, the likelihood that the variables are dependent becomes stronger, thus proving the null hypothesis incorrectThe following table would represent a possible input to the Chi square test, using 2 variables to divide the data gender and party affiliation. Chi square test, but in actuality any size grid would work as well 3x. Democrat. Republican. C Program Chi Square Test' title='C Program Chi Square Test' />Male. Female. This shows the basic 2x. However, this is actually incomplete, in a sense generally, the data table should include marginal information giving the total counts for each column and row, as well as for the whole data set. Democrat. Republican. Total. Male. 20. 30. Female. 30. 20. 50. Total. 50. 50. 10. Background Previous research has suggested that tai chi offers a therapeutic benefit in patients with fibromyalgia. Methods We conducted a singleblind, randomized. Contingency Tables Do different treatments cause different effects click here for exact, onesided analysis 2x2 contingency tables click here for other contingency. C Program Chi Square Test' title='C Program Chi Square Test' />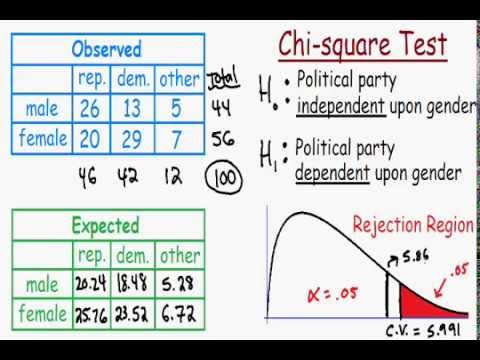We now have a complete data set on the distribution of 1. MaleFemale and party affiliation DemocratRepublican. A Chi square test would allow you to test how likely it is that gender and party affiliation are completely independent or in other words, how likely it is that the distribution of males and females in each party is due to chance. So, as implied, the null hypothesis in this case would be that gender and party affiliation are independent of one another. To test this hypothesis, we need to construct a model which estimates how the data should be distributed if our hypothesis of independence is correct. This is where the totals we put in the margins will become handy later on, Ill show how you can calculate your estimated data using the marginals. Meanwhile, however, Ive constructed an example which will allow very easy calculations. Assuming that theres a 5. Democrat. Republican. Total. Male. 25. 25. Female. 25. 25. 50. Total. 50. 50. 10. This is the information we would need to calculate the likelihood that gender and party affiliation are independent. I will discuss the next steps in calculating a Chi square value later, but for now Ill focus on the background information. Note you can assume a different null hypothesis for a Chi square test. Using the scenario suggested above, you could test the hypothesis that women are twice as likely to register as Democrats than men, and a Chi square test would tell you how likely it is that the observed data reflects that relationship between your variables. In this case, you would simply run the test using a model of expected data built under the assumption that this hypothesis is true, and the formula will as before test how well that distribution fits the observed data. I will not discuss this in more detail, but it is important to know that the null hypothesis is not some abstract fact about the test, but rather a choice you make when calculating your model. Trader Trainee Program here. What is the Chi square test NOT for This is also an important question to tackle, of course. Using a statistical test without having a good idea of what it can and cannot do means that you may misuse the test, but also that you wont have a clear grasp of what your results really mean. Even if you dont understand the detailed mathematics underlying the test, it is not difficult to have a good comprehension of where it is or isnt appropriate to use. I mentioned some of this above, when contrasting types of data and so on. This section will consider other things that the Chi square test is not meant to do. First of all, the Chi square test is only meant to test. It. will NOT tell you any details about the relationship between them. If. you want to calculate how much more likely it is that a woman will be a. Democrat than a man, the Chi square test is not going to be very. However, once you have determined the probability that the two. Chi square test, you can use. For a fairly. simple way of discussing the relationship between variables, I recommend. Some further considerations are necessary when selecting or organizing your data to run a Chi square test. The variables you consider must be mutually exclusive participation in one category should not entail or allow participation in another. In other words, the data from all of your cells should add up to the total count, and no item should be counted twice. You should also never exclude some part of your data set. If your study examined males and females registered as Republican, Democrat, and Independent, then excluding one category from the grid might conceal critical data about the distribution of your data. It is also important that you have enough data to perform a viable Chi square test. If the estimated data in any given cell is below 5, then there is not enough data to perform a Chi square test. In a case like this, you should research some other techniques for smaller data sets for example, there is a correction for the Chi square test to use with small data sets, called the Yates correction. There are also tests written specifically for smaller data sets, like the Fisher Exact Test. Degrees of Freedom. A broader description of this topic can be. The degrees of freedom often abbreviated as df. For a Chi square grid, the degrees of freedom can be said. You can see the idea intended if you have a given set of totals for. You can only fill in a certain amount of cells with random numbers before the rest just becomes dependent on making sure the cells add up to the totals. Thus, the number of cells that can be filled in independently tell us something about the actual amount of variation permitted by the data set. The degrees of freedom for a Chi square grid are equal to the number of rows minus one times the number of columns minus one that is, R 1C 1.